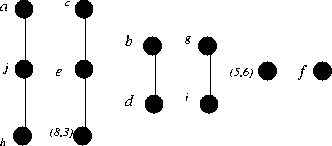MTH110
|
Assignment 2 Solutions
|

|
|
|
Tilomino Sets, Proofs and Relations
|
|
This page is best viewed in Firefox or Mozilla.
If you are having trouble reading some of the symbols in this page it probably
means that your browser is not HTML 4.0 compliant.
Part 1
1.0 Explanation
In ths question you will invent a new Tilomino world called N (i.e an 8
X 8 grid with tiles on it of the types allowed in Tilomino) which satisfies all the
properties 1 to 11 listed below. Properties 1 - 10 are those of question 3.2 of
Assignment 1, except
that numbers 7 and 9 have been changed slightly.
So here is a list of all the rules that it satisfies, each
is stated in both logical form and in English:
-
∀ y ∈ LABELS, ∃ x ∈ N, ROW(x, N) = y;
Every row has a tile in it.
-
∀ x ∈ N, ∃ y ∈ N, x ≠ y ∧ samecol(x, y) ∧
(∀ z ∈ N (z ≠ x ∧ z ≠ y) → ~samecol(x, z))
Every nonempty column has exactly two tiles in it.
-
∀ x, y ∈ TILENAMES, (x ∈ N ∧ y ∈ N ∧ larger(x, y))
→ x > y
Larger blocks have higher names.
-
∀ x, z ∈ N,
(x ∈ TILENAMES ∧ z ∈ TILENAMES ∧ x > z)
→ (∀ y ∈ TILENAMES, x > y > z → y ∈ N)
Tile names in N are consecutive.
There are no gaps in tile names.
-
∀ x, y ∈ N, COLOF(x, N) - COLOF(y, N) ∉ {-1, 1}
There are no blocks in adjacent columns.
-
(∀ x ∈ SHAPE, ∃ y ∈ N, x(y)) ∧
(∀ x ∈ SIZE, ∃ y ∈ N, x(y))
There is a tile of each size and shape.
-
∀ x, y ∈ N (samecol(x, y) ∧ larger(x, y))
→ (square(x) ∧ triangle(y) )
Given two blocks of differing sizes in the same column, the larger one is a
square and the smaller is a triangle.
-
∀ x, y ∈ TILENAMES
(x ∈ N ∧ y ∈ N ∧ x > y) →
(northof(x, y) ∧ (sameshape(x,y) → rightof(x, y)))
Higher named tiles are above lower named ones, if they are of the same shape
then the higher named ones are also to the right.
-
∀ x, y ∈ N, circle(x) → (rightof(x, y) ∨ circle(y))
Circles appear to the right of all other shapes.
-
COL(a, N) = 2 ∧ ~samecol(g, h) ∧ samecol(a, f)
a is in column 2 and so is f, but g and h are in different columns.
In addition it also satisfies the following rule:
-
small(e) ∧ large(g) ∧ triangle(b) ∧ triangle(c)
3.1 Number of tiles
What is the exact number of tiles in N?
Justify your answer using the properties 1 to 11.
(Hint: first show that this number is the minimum possible and then the
maximum possible).
Answer: 8
There are at least 8 tiles:
There is at least one tile in each row (1), so there must be at least 8 tiles.
There are at most 8 tiles:
At least every other column is empty (5), since there are 8 columns in
total, there are at most 4 nonempty columns. Every nonempty
column contains exactly 2 tiles (2), giving 8 tiles in total.
3.2 Identify all tiles
Complete the following table:
| Tile | a | b | c | d | e | f | g | h | i | j |
|---|
| Tile ∈ Na
| Y | Y | Y | Y | Y | Y | Y | Y | N | N |
|---|
| Size | S (3)c | S (3)c | S (3)c
| S (3)c | S (10)b | M (6)d
| L (10)b | L (3)c | . | .
|
|---|
| Possible Rowse | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | . | .
|
|---|
| Possible Columns
(2)(10) | 2 (10) | 4 (8)i | 6 (8)i
| 8 j | 8 j |
2 (10) | 4 (8)h | 6 (8)h | . | . |
|---|
| Shape | T (10)(7)f | T (11) | T (11) | Cj
| Cj | S (10)(7)f | S(10)(7)g
| S (10)(7)g | . | . |
Tile Names (Existence)
- We first note that a, h ∈ N (10) and so all names from a to h
must appear as well (4). These are the 8 tiles in N.
Sizes
-
e is small and g is large (11).
-
Larger blocks have higher names (3), so a to d cannot
be larger than e, and so must be small as well.
Similarly, since g is large h must be too.
-
Now all blocks except f have assigned sizes, but there are no
medium sized blocks. There is at least one tile of each size (6), and so
f must be medium.
Rows
-
Higher named tiles are above lower named ones (8). There are 8 named
tiles, a to h so they correspond one to each of the 8 rows in order.
Columns and Shapes
Each non-empty column has exactly 2 tiles in it (2) and so each tile
shares a column with at exactly one other. Columns adjacent to nonempty
ones are empty (5), since there are tiles in column 2 (10) the only columns
with tiles are 2, 4, 6, 8. Finally, the two tiles in col 8 are circles (6 and 9).
- We know that a and f are of different sizes (sizes above)
and they are both in column 2 (10), and so f is a square and a is a triangle
(7).
-
Consider the column containing h, it is not in the same column as g (10), and
hence is in a column with a smaller tile (g and h are the only large tiles by
sizes above). Thus h is a square above a triangle (7).
A similar argument shows that g is also a square which is above a triangle.
-
Since f, g and h are all squares, h is to the right of g (8) which is to the right
of f (8). None of them can be in the last column (since that must contain a
circle (6 and 9)). So f, g, h must appear in columns 2, 4 and 6 respectively.
-
By 2 and 7 there must be three small triangles in columns 2, 4 and 6, with
names from a to e, the one in column 2 is a (11). a, b and c are all triangles
so the higher the name the further right the tile (8).
-
This leaves d and e for column 8. Both of them must be circles (6 and 9).
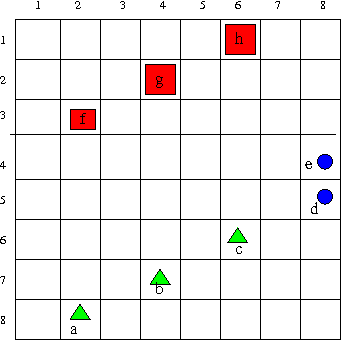
1.3 Place tiles in world
Now that you have identified all the tiles, place them in N so that all
the expressions 1 to 11 are true and all the other constraints listed so far are
satisfied. Do this with a drawing. You don't need to explain your answer, but
it must be correct. Note that there may be more than one possible solution.
Part 2 - Relations
2.0 Definitions
Given an arbitrary world W ∈ TILOMINOUNIVERSE we define
three binary relations RW, SW and
TW as follows:
-
∀ x, y ∈ W, x RW y ⇔
(samecol(x, y) & below(x, y)) |
x = y.
-
∀ x, y ∈ W, x SW y ⇔
~samerow(x, y).
-
∀ x, y ∈ W, x TW y ⇔
sameshape(x,y)
2.1 Specification
List the ordered pairs which make up the following relations:
-
RH
=
{ (a,a), (a,f), (a,b), (b,b), (c,c), (c,d), (e,e), (f,f), (f,b),
((2,2),(2,2)), ((2,4),(2,4)), ((7,6),(7,6)) }
- SR
=
{ (a, b), (a, c), (a, (6,8)), (b, a), (b, c), (b, (6,8)), (c, a), (c, b),
((6,8), a) ((6,8), b) }
-
TA
=
{ (a, a), (a, f), (a, e), (b, b), (b, c), (b, (2,4)), (c, c), (c, b),
(c, (2,4)), (d, g), (d, (2,2)), (e, a), (e, e), (e, f), (f, a), (f, e),
(f, f), (g, d), (g, g), (g, (2,2)), ((2,2), d), ((2,2), g), (2,2), (2,2))
((2,4), b), ((2,4), c), ((2,4), (2,4))}
2.2 Table
Fill out each cell of the following table with True or False.
(Note that the answers should be the same no matter what W is)
| Relation | Reflexive | Symmetric | Antisymmetric | Transitive
| Equivalence
relation | Partial
Order | Total
Order
|
|---|
| RW | T | F | T | T | F | T | F
|
| SW | F | T | F | F | F | F | F
|
| TW | T | T | F | T | T | F | F
|
2.3 Justification
The answers in this section refer to the table in the previous section.
Note that this section will be marked independently of the previous one. Thus
if your answer in the table are incorrect you will receive 0 for the
corresponding answer in this section.
Check your answers to the table carefully before continuing.
-
In each case where you answered True to Symmetric or
Antisymmetric provide a proof of the result. Be
sure to clearly state what you are trying to prove, both in English and
symbolic form and to justify each step as appropriate.
Note that in your proof you may assume that Tilomino functions act as described.
For example, suppose we know
then we now that x and y are in the same column,
and so we could make the statement:
| x and y are in the same column (Definition of samecol).
|
We can use the definitions in reverse as well.
Thus, if we know that x and y are in the same column in a world,
we can conclude
| samecol(y,x) (Definition of samecol).
|
-
RW is Antisymmetric.
To Prove ∀ x,y ∈ W, x TW y & y TW x
⇒ x = y
Proof
|
Let x,y ∈ W, with x RW y and
y RW x.
|
|
Thus (samecol(x, y) & below(x, y)) | x = y, and
(samecol(y, x) & below(y, x)) | x = y.
|
|
Noting that samecol(x, y) is equivalent to
samecol(y, x) and using distribution and negation gives
x = y | (samecol(x, y) & below(x, y) & below(y, x)).
|
|
But below(x, y) & below(y, x))
is a contradiction (Negation)
|
|
So x = y, (Elimination)
|
-
SW is Symmetric:
To Prove ∀ x,y ∈ W, x SW y ⇒ y SW x
Proof
|
Let x,y ∈ W, with x SW y.
|
|
Thus ~samerow(x, y). | (Definition of SW)
|
|
So x and y are not in the same row.
| (Definition of samesrow)
|
|
But then ~samerow(y, x). | (Definition of samesrow)
|
|
So y SW x | (Definition of SW)
|
- TW is Symmetric.
To Prove ∀ x,y ∈ W, x TW y ⇒ y TW x
Proof
|
Let x,y ∈ W, with x TW y.
|
|
Thus sameshape(x, y)
| (Definition of TW)
|
|
So x and y are the same shape.
| (Definition of sameshape)
|
|
Thus sameshape(y, x).
| (Definition of sameshape)
|
|
So y TW x. | (Definition of TW)
|
- In each case where you answered False to Reflexive,
Symmetric, Antisymmetric or Transitive give a world
from the Tilomino program { F, 2, R, A, B, S, H } where the property
fails, identify why the property fails in that world.
- RW is not symmetric:
World A, a and b are in the same column, and below(a, b), so
(a RA b)
but ~below(b, a) so ~(b RA a)
(Same for any other pair of tiles one below the other in the same column in any world.)
-
SW is not Reflexive:
World A, a is in the same row as itself, so
~(a SA a).
(Same for any tile in any world.)
-
SW is not Antiymmetric:
World A, (g SA a) and
(a SA g), but a ≠ g
(Works for any pair of distinct tiles.)
-
SW is not Transitive:
World A, (a SA g),
and (g SA d),
but ~(a SA d).
(Works for tiles x, y and z, with x and z in the same row and y not.)
-
TW is not Antisymmetric:
In world A, (b SA c), and
(c SW b), but b ≠ c
(Works for any pair of tiles not the same shape.)
-
In each case where you answered True to Equivalence relation:
Describe an arbitrary equivalence class, [x], x ∈ W,
both as a set and in English.
[x] = { y ∈ W | x and y are the same shape }
or
[x] = { y ∈ W | sameshape(x, y) }
[x] is the set of tiles which are the same shape as x.
-
In each case where you answered True to Partial Order or
Total Order, for W = B:
-
Give the Hasse diagram.
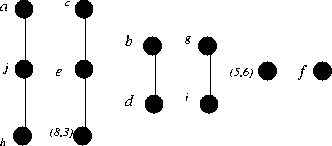
-
Specify any greatest or least elements.
There are no greatest or least elements.
-
Identify all maximal and minimal elements.
a, c, b, g, f and (5,6) are all maximal elements.
h, (8,3), d, i, f and (5,6) are all minimal elements.
-
If possible give two non-comparable elements which are neither
maximal nor minimal.
j, e.
-
Where possible give:
-
A chain of length 1, which is not contained in a chain of length 2.
{g, i}, or {b, d}.
-
A chain of length 2, which is not contained in a chain of length 3.
{a, j, h}, or {c, e, (8,3)}.
-
A chain of length 3, which is not contained in a chain of length 4.
There are no chains of length 3.
Hand in
-
A writeup of your answers to all questions.
-
The Assignment 2 Marking Sheet
(To Appear)
stapled to the front of your assignment.
Maintained by Peter Danziger.
This page is best viewed with Mozilla Firefox.
Last modified
Tuesday, 08-Dec-2009 16:02:16 EST